EEK! All those negatives and positives! And, I have to add and subtract them? I can't get them straight!

Do YOU feel that way when you see a bunch of + + – – + – + signs? You are not alone. It can be totally confusing and there are a number of ways to add and subtract integers—teachers will usually teach one method but YOU have to learn the method that works best for Y-O-U! Each of our brains works a bit differently and with integers, since they tend to be soooooo confusing, find the method that sticks in YOUR brain and go for it! Soon, you will find that integers really aren't so hard after all.

OH, and why are both addition AND subtraction all stuck on one page here? hmm…I think you will see the connection soon enough!

The ABSOLUTE VALUE method often works for some folks and since absolute value was such an easy-peasy concept then maybe it will work for you.

Walking from zero wasn''t so hard to do…So, let's USE that knowledge for operating with addition and subtraction. Let's begin by taking a look at addition.

The first time you deal with integers you are probably working with only the positive integers. So, to make things super-simple, we'll stick with just the positive integers for our example.

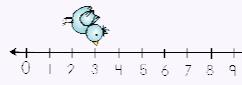
The first addend (3) tells you where to begin.

Our bird starts on the 3. Now, we see a + sign so we are ADDING or moving to the RIGHT.

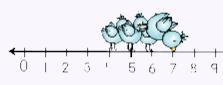
Looking at the number after the + sign, we see a 4. The absolute value of the 4 is…4 so, birdie is going to walk 4 steps to the right.

Where did the little bird end up? On the 7! Yaaa-hooo! So, 3+4=7

You're probably thinking to yourself, "HEY, I know what to do with the POSITIVE integers…I want to learn what to do when I've got all those negatives and positives all over the place!" Relax…it isn't difficult at all, particularly if you know the basics when it comes to addition!

If you stop and think about what you were really doing back in elementary school, you were adding the absolute values of the addends of those positive integers. Yes, you were! And, the sum is…positive, right?

So, using this information, try it with negative numbers and see what happens. We'll continue with our bird friend.

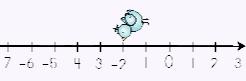
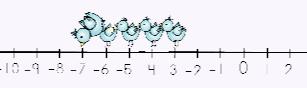
Where does your little bird start? The first addend tells you he will begin on the -2.

The plus sign (+) tells you to move to the…RIGHT. But, oh no! There's a -5 this time!

Take the absolute value of the -5 which is 5.

The problem is that NEGATIVE sign. Think to yourself: +-. Negatives always over-power positives so this means birdie is actually going to the LEFT, not right.

So, how many spaces is he moving to the left? Five! What is our sum?

Voila! So, -2 + (-5) = -7

When you are adding two negative numbers, your sum will be a negative.

"There just HAS to be a better way to add and subtract integers," you're probably thinking, right? Well, like I said, there ARE a lot of ways to do compute with integers. MY preferred method is through the use of patterns and drawing pictures, and don't worry, you don't have to be an artist with this method. You just have to be able to draw a triangle.

Step #1: Draw the triangle

Draw an upside-down triangle.

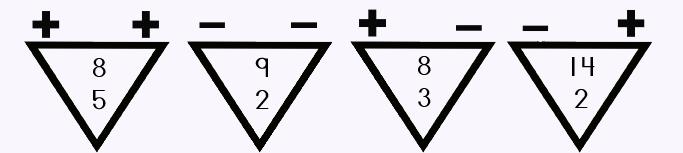
Step #2: Re-write the problem

This is the hardest part. (NOT!) Look at the numbers in the problem and IGNORE the signs.

Which number is the BIGGEST number? Write that number first.

Now, write the smaller number under the big number.

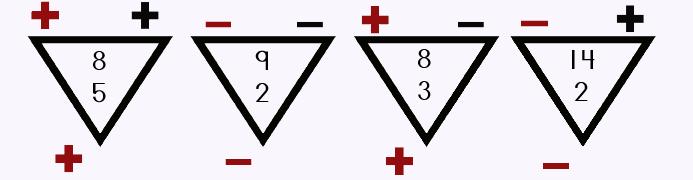
Step #3: Write the signs

Look at the original problem.

What sign went with the big number? Write that sign first on the top of your triangle.

What sign went with the little number? Write that sign next on the top of your triangle.

NOW, at the bottom of your triangle, write down the SAME number you wrote first! This is the sign your answer will be.

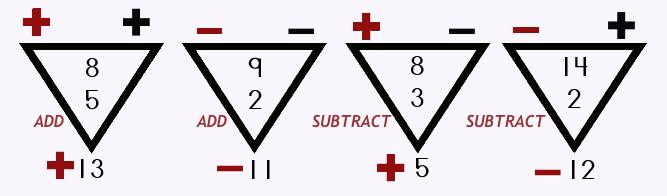
Step #4: Do the math

Look at the signs at the top of your triangle.

ADD if you have a matching pair (+ + or – –)

SUBTRACT if you have a mismatched pair (+ – or – +)

That's it!
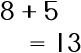
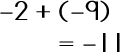
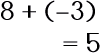
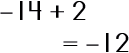