What are integers? Integers are the counting or natural numbers (1, 2, 3, …), their negative partners/opposites (–1, –2, –3, …), and the number 0.

We can use set notation to show integers like this:: {…–3, –2, –1, 0, 1, 2, 3, …} or, if you are more into visuals, you can use a number line.

On a number line it is clear to see that there are positive and negative integers along with the number 0.

As you move to the right of the number line, the numbers get bigger.

As you move to the left, the numbers get smaller.

Now, do you see any fractions on this number line? How about decimals?

Did you answer, "No," and "no"? If so, then you are correct! Fractions and decimals are not integers so they are not part of the integer family.

Using the number line, it is easy to compare integers. We use certain symbols when we compare integers:

< (less than) and > (greater than)

< (less than or equal to) and > (greater than or equal to)

Now, the easiest way to remember HOW to make that symbol when comparing integers is to use a little trick with dots. Look at EACH number.

The smallest number or the number furthest to the left on the number line gets ONE dot.

The largest number or the number furthest to the right on the number line gets TWO dots.

Now, connect the dots, like in a dot-to-dot, and you've drawn your symbol! (answers: > and <)

See if you can figure out what the answers are to a few integer comparisons.

Use the number line to help you. Use the symbols < and > to make each statement true.

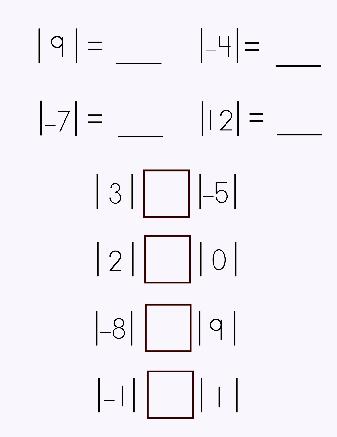
Absolute value, simply put, is the distance a number is from zero. Two vertical bars are used to denote absolute value, i.e., |–3|. Since absolute value indicates the 'distance from zero,' it is always going to be a positive number. Absolute value is useful when computing with integers.

The |–3| = 3. Interestingly enough, the |3| = 3. Remember, the absolute value is how far from zero a number is! This means, it doesn't matter if a number is a positive or a negative integer; its absolute value is going to be a positive number. Period. Think about it. Why would it be a positive number? (distances can't be negative, right?)

Did you wonder about the number 0? What would the absolute value of 0 be? Take a wild guess! Go ahead…

The answer: the absolute value of zero is zero. That's right! Cool, huh?

See if you can figure out the answers to the following:

©2011–2017 Sherry Skipper Spurgeon. All rights reserved.