Some function rules follow a specific form. We learned the relation for linear equations was y = mx + b. There are other function relations that have specific rules and we will learn in pre-algebra called 'direct variation.'

We have already learned that a linear equation takes the form y = mx + b. In that particular function or rule, the constant is b, and this constant is also the y-intercept. The slope is denoted by m.

WELL, a direct variation is in the form y = kx. Hmmm… Look familiar? Of course it does! Check it out. Let's just compare the direct variation function rule to the linear function rule for a second…

Notice any similarities? Differences? The linear equation has + b and the direct variation doesn't…and instead of m for a coefficient, the direct variation uses the letter k.

So, what does this tell you about the function of a direct variation? (THINK!)

It tells us that a direct variation is…a LINEAR EQUATION! And, the slope is represented by k (why the powers that be didn't stick with the letter m is beyond me! It would have made things so much easier, right? Oh well, why makes things TOO easy…).

Can you figure out what the y-intercept of each and every line is? This shouldn't be too difficult…Did you guess (0, 0)? You'd be correct! The reason for this is simple to determine if you follow the logic of the linear equation function. Since there is no "+b" then it stands to reason that the y-intercept is (0, 0).

Let's see some of the ways you can determine a direct variation.

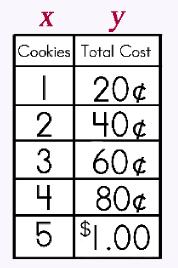
Here is the price list for cookies at Le Bakerie. Is this a direct variation?

In a table, you can write the columns to fit a coordinate grid format by writing one column to represent the x-axis (the 'input' or domain) and the other to represent the y-axis (the 'output' or range). You can then check each to make sure there is indeed the same number (is the number 'constant?') between the values.

Let's take a look at the data in this table.

If we take the data and re-write we can see if we do have a constant. Let's see…

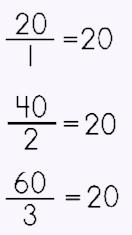Yep, we do have a constant! The ratio is 20 each time so that means the constant of variation is 20. This IS a direct variation!

k = 20

This means we can write a function rule!

Now that we know that data shows a direct variation, we can write a rule or function or equation to show this. All direct variations follow the same form, y = kx, so we can put our rule in that form by simply SUBSTITUTING our constant (k) into the form!

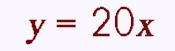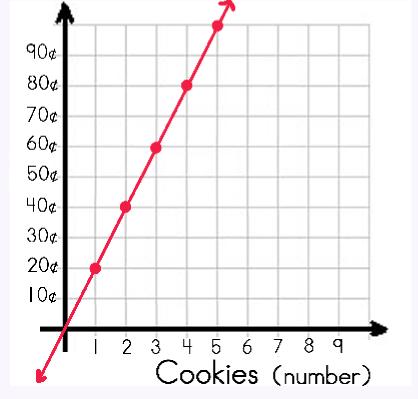
We can even graph our results.

Check out the graph…

What is the y-intercept? Ahh…did you notice that the line intercepts the y-axis at 0?

Yep, right at (0, 0)!

Note: In math books, the authors will explain it this way: "The variables y and x are said to vary directly with each other. The constant k is the coefficient that causes a variation to occur, making the x change," but I think it makes more sense to see it as a linear equation since in a linear equation you already know that the the variable x is directly effected by a constant (the slope)

Have you ever see a problem like this…

Write an equation of the direct variation from the given point. (5, -10)

What was YOUR reaction? Probably, "Huh?" Yeah, a typical response! This problem is WAY easier than you initially thought because you actually have ALL the information you need right in front of you! Keep in mind that ALL direct variations follow the same ol' format:

You already know a property that you can use. Think! Did you say, "Substitution Property" or something like that? Hooray!

The numbers in the the ordered pair (5, -10) are in the form (x, y), so simply subsitute them and then solve for k !

What is easier, you may be wondering, right? Think about it! Solve for k in the equation FIRST like this:

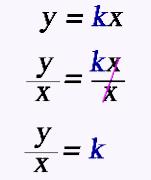Start off with the form for a direct variation.

Use the Division Property of Equality to move the x over to the other side.

Voila! Now, you can see how to get the constant of variation using your ordered pair!

We are going to go back now to that confusing math problem to see how to use this 'new' equation that really isn't new.

The problem was:

Write an equation of the direct variation from the given point. (5, -10)

Let's put our numbers into our 'new' equation, shall we?

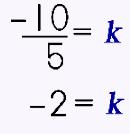Okay, so we substitute the -10 for the y in the numerator's place.

We substitute the 5 for the x in the denominator's place.

We can reduce the fraction to -2.

Voila! We now have our constant of variation or k!

Since we need to write an EQUATION for the direct variation, we just substitute our newfound k in place of the k in the equation and we are finished.

©2011–2017 Sherry Skipper Spurgeon. All rights reserved.