Order of operations refers to the order in which you 'do the math.' It is a convention (agreement or generally-accepted standard) for how the math is done.

Here's the deal: you want consistency in math, right?

Simplify this expression without a calculator.

Now, try it with a calculator.

Did you end up with two different answers? Probably, right? Why is this? Hmm…Let me explain!

If we go strictly with the notation (written), then we need to have a convention or an agreed-upon order in how to simplifying the expression and the real reason is because of the Distributive Property! Multiplication has 'power over' addition so if you have any multiplication in an expression, you need to group and do these. A-ha!

So, then the above problem should be simplified as:

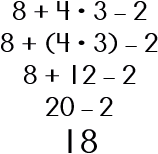The generally accepted convention for order of operations is to do all operations within parenthesis first followed by exponential notation, multplication then division (left-to-right), and addition and subtraction from left-to-right.

The acronym PEMDAS (Please Excuse My Dear Aunt Sally) was designed to help students remember this conventional 'order'as they simplified expressions: parenthesis - exponents - multiplication - division - addition - subtraction.

A similar acronym, BEMDAS (Brackets Exponents Multiplication Division Addition Subtraction) is the same thing but with the B exchanged for the P for parenthesis.

An acronym that I prefer is GEMA (Grouping Exponents Multiplication Addition). Now, why did I not include division and subtraction in my acronym? It's simple~we are always using the inverse of these operations when simplifying expressions in pre-algebra so it is a 'given,' as far as I am concerned so why nit-pick over a letter or two? You should have this ingrained by now and the acronym is simply to help remind you that order matters.

If you need an additional reminder, then the grasshopper should do it:

Grasshoppers Eat Most Anything

Let's see how we use GEMA to simplify a problem or two.

Simplify each of the following:

Step #1: Grouping

Check for grouping symbols aka the Distributive Property.

Do the math within any grouping symbols. ( ) [ ] { }

no grouping symbols

Distributive Property

Step #2: Exponents

Next, come the exponents.

no exponents

no exponents

Step #3: Multiplication/Division

Any multiplication/division is done next from left-to-right.

Step #4: Addition/Subtraction

Last comes all addition/subtraction from left-to-right.

©2011–2017 Sherry Skipper Spurgeon. All rights reserved.